The Voltage Model

Preface

This idea came about when multiple teachers & professors insists on calling it voltage levels, which lead to the question, why call it levels?

It sparked the idea that you can represent voltage with height, in which is true!

You can indeed do that, however, that leaves us with the question of how we interpret this new idea in this new dimension.

Motivation

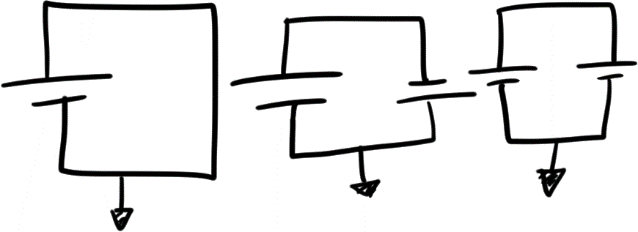
Consider the following circuits on the right in an ideal environment.

A simple question would be, at what voltage values would make these valid?

Forget Ohm’s law, we can instantly visualize which of work and which don’t in certain conditions. This is because we’re tackling these in the realm of visuals, not formulas.

This doesn’t mean you throw away all formulas, they are still important if you want to get a mathematically correct answer!

3D Visualization Entrée

Example 1.1

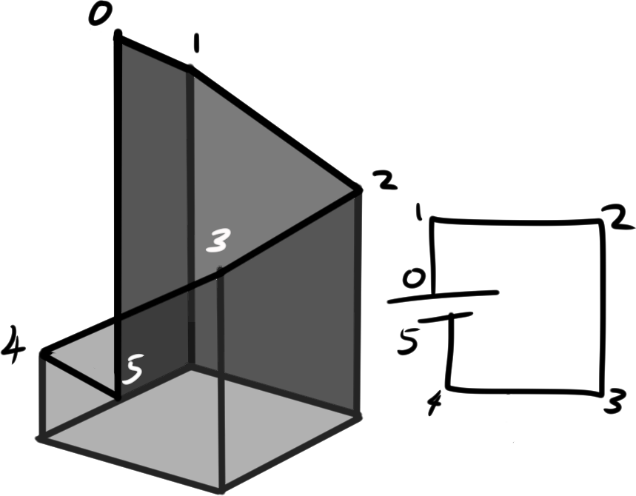
Let’s start by understanding what happens in the circuit on the far left when we translate it into a 3D realm.

The mapped points here are matching, so you can somewhat visualize the process of transforming it.

As you may notice, the slope of the diagram here represents the current, so the steeper the slope, the larger the current.

Rolling Ball

As many books have depicted, an electron is like a ball, we can somewhat visualize an electron rolling down this circuit. However, one should note that it doesn’t “accelerate” like a real ball, its speed is proportional to the slope.

“Non-Ideality”

As you may notice, if we were to consider this to be in an ideal environment, the slopes should tend to infinity as ideal wires have zero resistance. So, what you’re seeing here is non-ideal.

Energy Released

Since the electrons are going at such a fast speed downwards, we can predict that the energy released is going to be exceptionally large, in which is true! The low resistance of the wire makes it such that electrons are zipping through the circuit without resistance.

Example 1.2

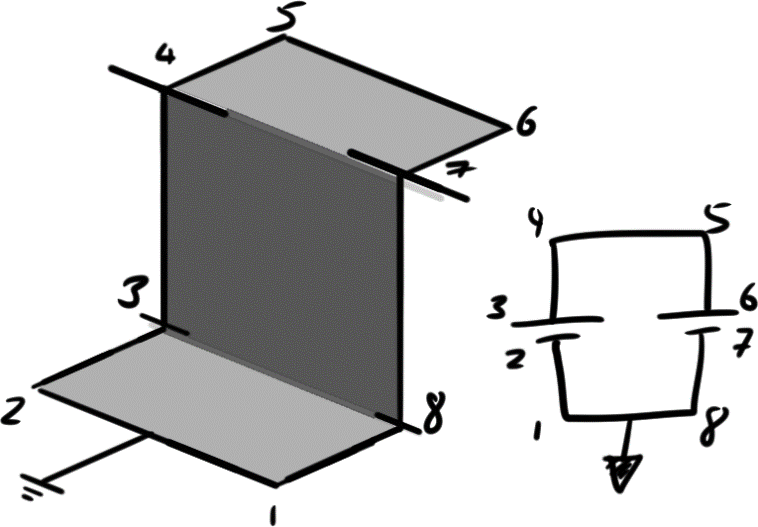
Before we get into resistors (as foreshadowed), let’s consider another example that we looked at before.

What voltage values would make these valid?

I think this is a simple question now, if we were to consider that we don’t want electrons speeding across the circuit, we must keep all wires on the same level.

Hence the only ideal condition where this circuit works is if both voltage sources have the same voltage difference!

Consider the figure on the right, (1,2,3,8) and (4,5,6,7) are grouped on their respective voltage levels. Where (1,2,3,8) are on the ground level.

Voltage Relativity

A common question is why can we just assign a random spot on the diagram as the ground?

What makes it a ground and why is voltage relative?

Consider the above diagram and compare it to this.

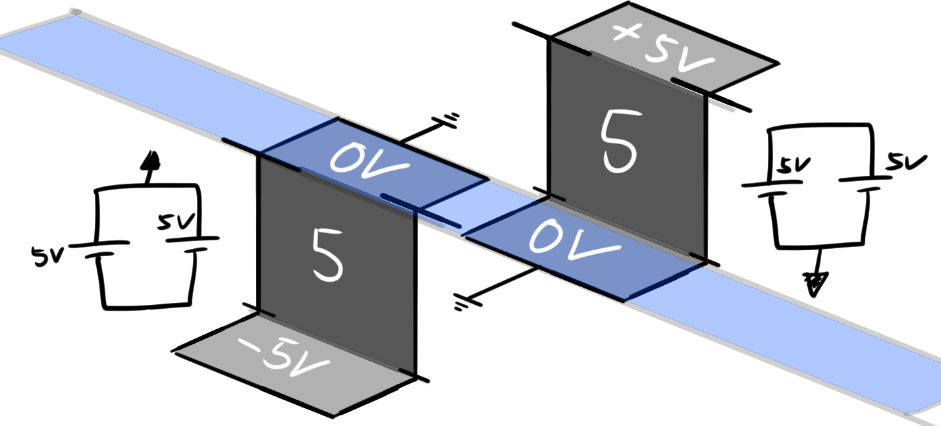
Notice that if you’d just move the diagram up, you get a diagram with totally different level values.

We made the voltage difference of the sources 5V for simplicity.

Therefore, can we randomly assign a spot to be a “ground”? Yes, but make sure that the rest of the circuit follows that reference!

Resistor

Consider the very first example again, what if we added an infinite amount of wire in that ideal environment?

We will slow down the electron balls because the slope is so gentle!

If we were to squish this infinite wire to a simple singular component, it’s called a resistor. (This is an analogy!)

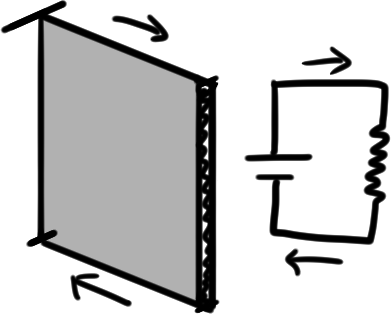
A resistor is a bit odd since it looks like it does provide a Voltage increase but note it will only decrease voltage in the direction of the ball rolling (the current).

In other words, if we were to flip the voltage source only, the ball will start to roll in the other direction. Just like a wire, it’ll flip itself to make sure that the ball is rolling in the opposite direction.

Example 2.1

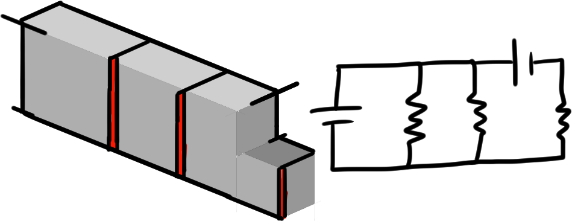
Let’s start by trying out different circuits

This may look complicated but after drawing it out, it paints a much simpler picture than that of a circuit diagram.

Always note that the height is equivalent to the voltage, so if you want to find any current through any resistor here, you’d just have to apply $V = IR$ where $V$ is the height.

Example 2.2

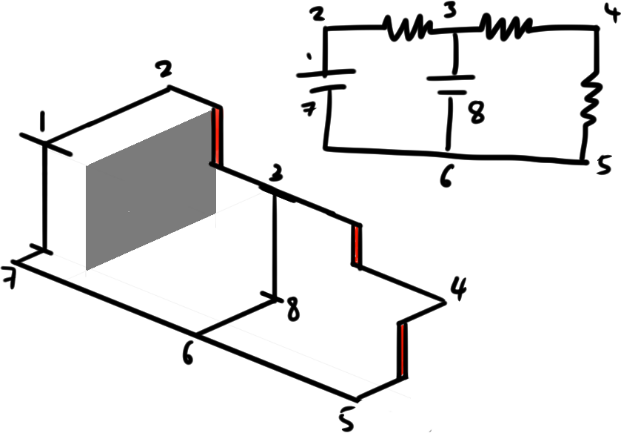
Sometimes drawing it out is hard, you may get the perspectives wrong like the following here. However, do not get confused between bad art and invalid circuit.

If you understand that it’s physically possible, you don’t have to get it right all the time.

Numbering the landmarks on your diagram may help you if you do get a complicated circuit drawn horrendously.

Working with Values

Up till now, we didn’t analyse circuits with values because it’s more interesting to look at diagrams. However, let’s now look at some actual circuit analysis problems.

We’ll first look at the classical way of circuit analysis, then use our 3D model to verify, just as a safety-net.

Example 3.1 (Classical)

Voltage

Since the voltage is divided between the 2 resistors, the voltage above $4\Omega$ is $\left( 3*\frac{4}{2 + 4} \right)V = 2V$.

Current

The current is just $I = V/R$. $I = \frac{3}{2 + 4}A = \frac{1}{2}A$.

Example 3.1 (Model)

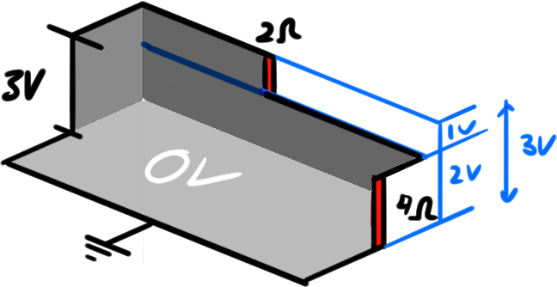
Voltage

Notice how the $4\Omega$ resistor takes up double the Voltage height compared to $2\Omega$? It’s like how it has “double” the length of wire for the electron ball to roll through. We can quite literally visually calculate the voltage between the 2 resistors.

Current

Current is usually the harder one to find visually since it doesn’t directly model it. However, as a rule of thumb:

Any node to any other node has the same current.

That is, if your current doesn’t “split” it is guaranteed that the current is the same. It’s good to look up Kirchhoff’s Current Law for this if you aren’t clear.

For this, we resort to Ohm’s law, which states $I = V/R$. We can sort of visualize the relative amount of “infinite length wires” each resistor uses, 2x and 4x. Since they are on the same loop, we can add them up without any discrepancies, we end up with a 6x “infinite length” loop.

As a result, we get $I = \frac{3V}{6X} = \frac{1}{2}*\frac{V}{X} \approx \frac{1}{2}A$.

To make it more concrete, we can substitute x with ohms to fit with Ohm’s law